目标
解决分布式缓存问题
例如数据库场景中,添加一个备份服务器时,如何将已有数据根据某列重新均衡
哈希环
算法
-
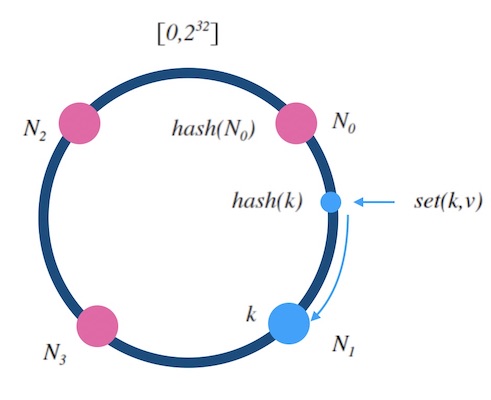
设$hash(x)$是映射到区间$[0, 2^{32}-1]$上的一个哈希函数,把区间首尾相连,形成一个顺时针增长的哈希环
-
将所有槽位$N_0$,$N_1$,…,$N_{n-1}$的标号$0$,…,$n-1$依次作为$hash$函数的输入进行哈希,把结果分别标记在环上
-
对于输入k的映射,求出$hash(x)$,标记在环上:
a. 如果$hash(x)$刚好落到槽位上,返回槽位标号
b. 否则, 顺时针沿着环寻找离$hash(x)$最近的槽位,返回槽位标号
添加删除节点
-
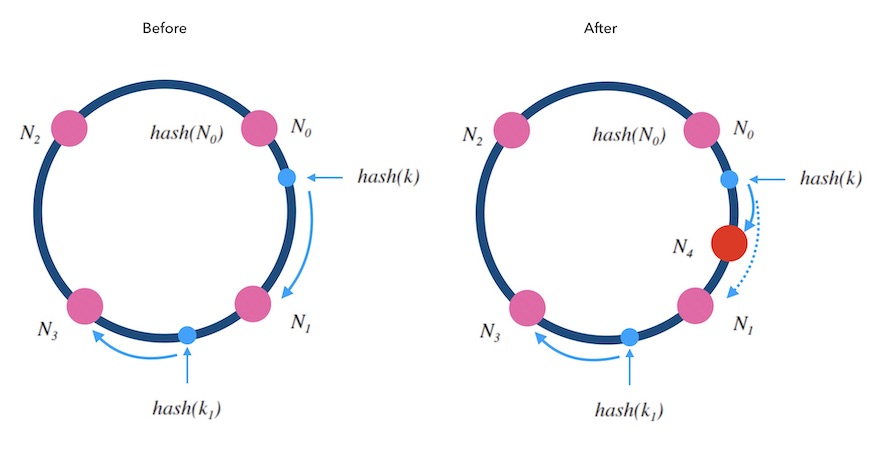
添加槽位$N_4$到$N_0$和$N_1$之间
-
对于所有$hash(N_0)<hash(x)<=hash(N_4)$的$x$,更新标记为$N_4$
对于kvdb的例子而言,就需要把$N_1$上所有的满足条件数据迁移到$N_4$后才能重启服务
删除同理于添加,略
均匀性
不均匀,哈希环强依赖槽位的手动划分
复杂度
核心点在于如何查找$x$的槽位,由于哈希环本质是一个连续的自然数轴,我们可以用二分法寻找,因此时间复杂度为$O(log(n))$
空间复杂度为$O(n)$
权重
通过影子节点实现,例如我们可以设置$N_m$和$N_n$对应一个编号&l&,但实际上这两个槽位是分开的
热扩缩容和容灾
扩缩容都需要在涉及的节点完成数据迁移后才能正常服务
备份可以将数据备份写入顺时针的下一个节点内
跳跃一致性哈希法
1
2
3
4
5
6
7
8
9
int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
int64_t b = -1, j = 0;
while (j < num_buckets) {
b = j;
key = key * 2862933555777941757ULL + 1;
j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
}
return b;
}
源代码用到了线性同余法求随机数列,属于很基础的随机数生成法,这里不再展开
算法
和哈希环算法不同,一致性哈希法本质是$ch(x, n)$,其中$x$是输入的键(整数),$n$是槽的总数,$X$是映射的数据总数量,该函数输出需要进入的槽编号
每次槽的数量从$i$变为$i+1$时,如果数据分布完全一致(即每个槽数据量一样),则需要有$X/(n+1)$个数据需要重新映射
伪随机数可以保证种子不变的情况下随机序列不变,但是随机序列内的元素都能保证随机分布
因此:
- 对每个元素$x$通过随机生成算法$M$生成一个随机序列$M^x_i$,其中$i\in\mathbb{N}$
- 在槽位数量从$j$增加为$j+1$时,判断$M^x_j$是否小于$1/(j+1)$,若小于则移动元素$x$到槽$j+1$,否则不移动
1
2
3
4
5
6
7
8
int ch(int x, int n) {
random.seed(x);
int b = 0; // This will track ch(x, j+1).
for (int j = 1; j < n; j++) {
if (random.next() < 1.0/(j+1)) b = j;
}
return b;
}
但其实对于每个元素$x$,槽位增加到$j$时,$x$移动的概率是很低的,我们知道当$x$从某一时刻换到$i$槽后,一直从$i+1$槽开始累计不移动直到$j$槽的概率为
$P(i, j)=\frac{i}{i+1}\times\frac{i+1}{i+2}\times{…}\times\frac{j-1}{j}=\frac{i}{j}$
在随机序列一致的情况下,我们无需不断生成$x$的随机序列,可以在第$i$次换槽后用$\frac{i}{j}$和下一个随机数$M^x_k$来判断$x$可以在槽位$i$停留多少次。而更进一步,随机数$M^x_k$要满足$M^x_k<i/j$,那么$j<i/M^x_k$,因此算法可以改进为:
- 若$x$换到槽位$i$或$i=0$,生成$x$为种子的随机数序列的下一个随机数$M^x_k$
- 如果输入的槽位数量$n$小于$floor(i/M^x_k)$则返回$n$,否则移动$x$到$floor(i/M^x_k)$并重复步骤1
1
2
3
4
5
6
7
8
9
10
int ch(int k, int n) {
random.seed(k);
int b = -1, j = 0;
while (j < n) {
b = j;
r = random.next();
j = floor((b+1) / r);
}
return b;
}
均匀性
均匀,符合随机分布
权重
通过影子节点实现,同哈希环
复杂度
每个元素$x$的期望跳跃次数为$\lim_{n \to \infty }\sum_{2}^{n}\frac{1}{i}$,算法的时间复杂度为$O(ln(n))$,优于哈希环
空间复杂度为$O(1)$
热扩缩容和容灾
扩缩容:
-
无法自定义槽位符号,只能自增标号
-
只能在尾部增删槽位
容灾和哈希环类似:
-
尾部节点备份一份数据到老节点
-
非尾部节点备份一份数据到右侧邻居节点
Maglev一致性算法
算法
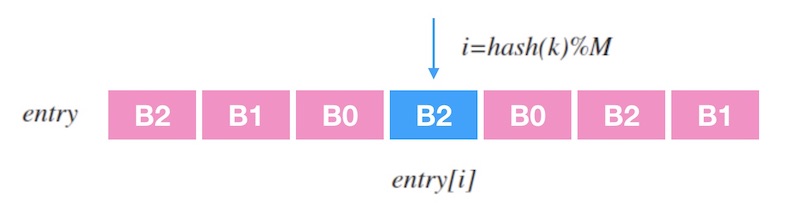
maglev的思路是查表,对于一个输入$x$,我们计算$hash(x)\%A$得到一个$[0, A)$的整数,根据离散列$entry$得到最终的槽位$entry[hash(x)\%A]$
假设我们有三个槽位$N_0$,$N_1$和$N_2$和长度为$A$的离散列$entry$,我们给槽位$i$生成一个长度为$A$的偏好序列$M^i$。然后依次让槽位根据自己的偏好序列$M^i$映射到$[1, A]$中,具体流程如下:
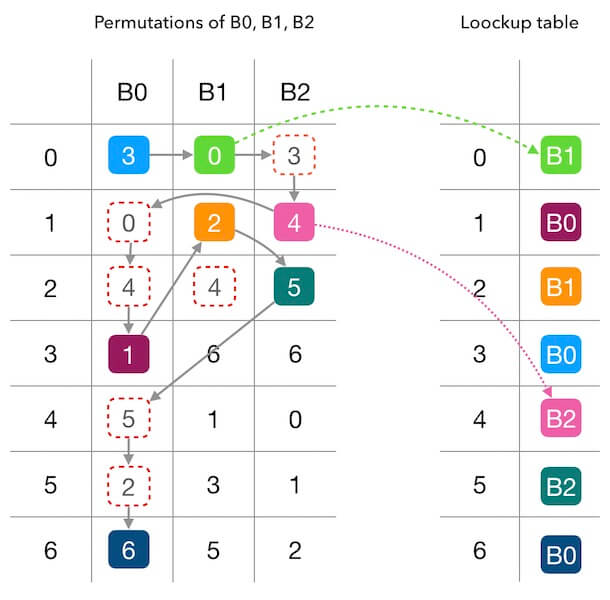
- 查找0号槽位序列的第1个数字$M^0_1$
- 标记$entry[M^0_1]=0$
- 对1号槽位如果$entry$[$M^11$]被标记,则顺延至1号槽位序列第$a_1$个数字$M^1{a_1}$满足$entry$[$M^1{a_1}$]未被标记,并标记$entry$[$M^1{a_1}$]$=1$
- 对后续槽位重复第3步
例如对于下图,$A=7$,$M^0$为$[3,0,4,1,5,2,6]$,$M^1$为$[0,2,4,6,1,3,5]$,$M^2$为$[3,4,5,6,0,1,2]$,最终得到$entry$映射表为$[B_1,B_0,B_1,B_0,B_2,B_2,B_0]$
偏好序列的生成采用二次哈希的方法:
$offset=h_1(x)\%A$
$skip=h_2(x)\%(A-1)+1$
$i$号槽位的偏好序列生成为$M^i_j=({offset}+j\times{skip})\%A)$
其中,我们需要保证$A$是一个质数,这样可以减少哈希值的聚集和碰撞
maglev的重新映射没有做到最小化,每次增删槽位都需要重新生成映射表$entry$,并根据映射表的变化重新修改数据和槽位的映射关系。不过,在Google的实际测试中总结出来,当查找表的长度越大时,maglev哈希的重新映射消耗越小
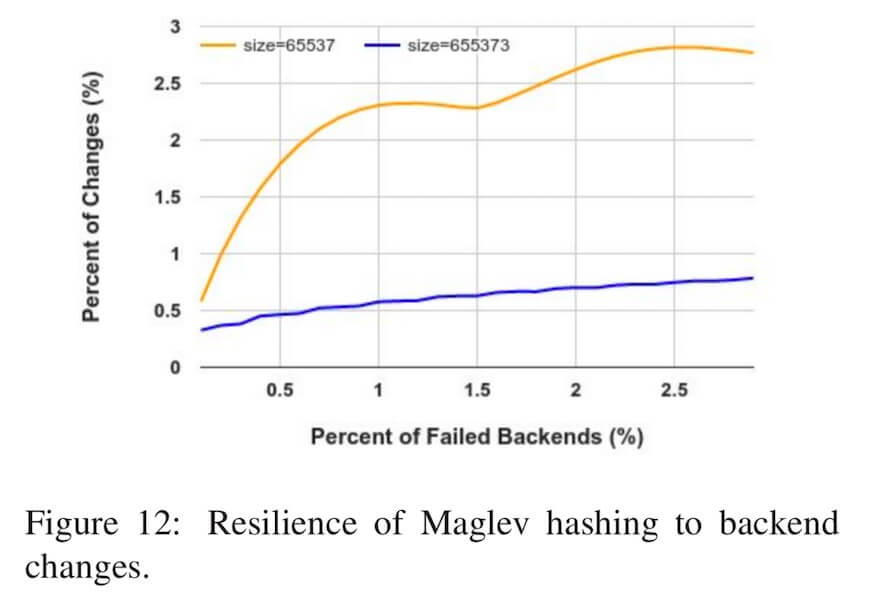
在Google实践中,一般选择$A>100\times{N}$($N$为槽位数量),这样各个槽位在查找表上的分布的差异就不会超过$1%$
复杂度
查找的时间复杂度$O(1)$
查找的空间复杂度$O(A)$
生成查找表$entry$的时间复杂度为$\sum^A_{i=1}\frac{A}{i}$,因此为对数级别$O(Aln(A))$
权重
可以从生成$entry$的顺序做加权,例如$1$号槽位连续填3次
热扩缩容&容灾
扩缩容重新生成&entry&表来腾挪数据,具体如上几节所述,热扩缩容时保留一份老的映射表来保证可以读到数据
容灾也可以通过顺序槽位的方法创建备份
算法对比
| 均匀性 | 最小化重新映射 | 时间复杂度 | 加权映射 | 热扩容 & 容灾 | |
|---|---|---|---|---|---|
| 哈希环 | × | √ | $O(log(n))$ | √ | √ |
| 跳跃一致性哈希 | √ | √ | $O(ln(n))$ | √ | √ |
| Maglev哈希 | √ | × | $O(1)$ | √ | √ |
参考
https://writings.sh/post/consistent-hashing-algorithms-part-1-the-problem-and-the-concept