如果你期待这里是哥德巴赫猜想的证明啥的,那你可能要失望了,这里只是一个纯粹的自然数加法证明。
引言
15年前,和同学闲聊的我被一个问题难住了。
1
2
3
4
5
:1+1等于几?
:2
:1+1为什么等于2?
面对这个问题我一时语塞,对于一个没接触过高等数学的中学生来说,这种抽象的问题没有任何切入点和思路,我甚至回家后还搜索了百度,但是也没得到自己满意的答案(当然如果那个时候我学会科学上网,就是另一个结局了)。
于是乎,这个问题就成为了陪伴我这几十年来的疑惑,也成为了我对数学爱好的起源(之一?),甚至可以说我当年填报专业选择数学也是有这方面的因素。当然,本科阶段的学习过后我就明白为啥1+1等于2了,不过我一直想找个机会用最直观最简单的方式把1+1为什么等于2解释给15年前的我,这也是我写这篇文章的初衷。
定义自然数
首先,我们思考一个问题,为什么自然数域$\mathbb{N}_0$是一个可数无上界无穷的集合?为什么自然数的增长顺序是

而不是以下这些呢?
因为事实就是,自然数是被定义出来的
为了理解这个定义过程我们需要抛弃原有的自然数认知:1并不是本来就存在的,1只是一个符号,它代表的就是0的后继数(这个后面会展开),同理2也是。0,1,2,3的增长顺序并不是因为它本身就长这样,而是数学家定义了自然数后,用1,2,3,4,…这串符号来代表每个自然数域中的每个数,并让这个数字系统变为标准
那么,自然数是如何定义的?
自然数的定义其实就是皮亚诺公理:
-
$0$是自然数;
-
每一个确定的自然数$a$,都有一个确定的后继数$S(a)$,$S(a)$也是自然数;
-
对于每个自然数$b$、$c$,$b=c$当且仅当$S(b)=S(c)$;
-
$0$不是任何自然数的后继数;
-
任意关于自然数的命题,如果能证明:它对自然数$0$是真,且假定它对自然数$a$为真时,可以证明对$S(a)$也真。那么,该命题对所有自然数都为真。
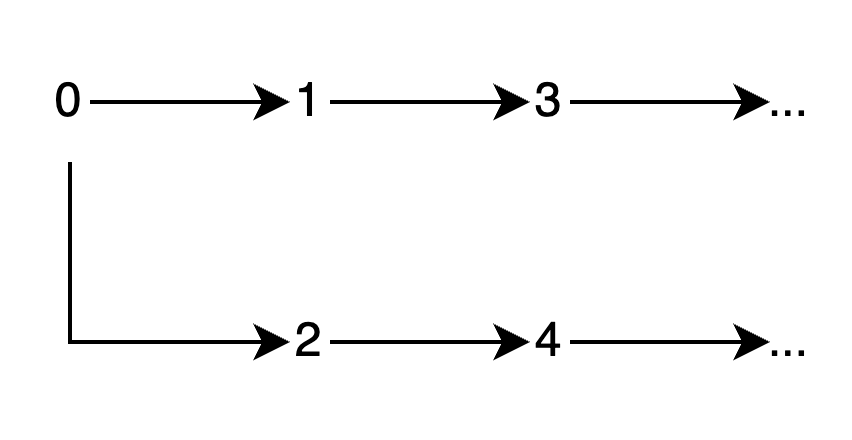
公理2的定义告诉我们,自然数的增长是唯一的,一个数的后继数不可能有两个,因此图2所示0的下一个数同时是1和2的情况就不可能存在了,即自然数的增长不会出现”分岔“了。
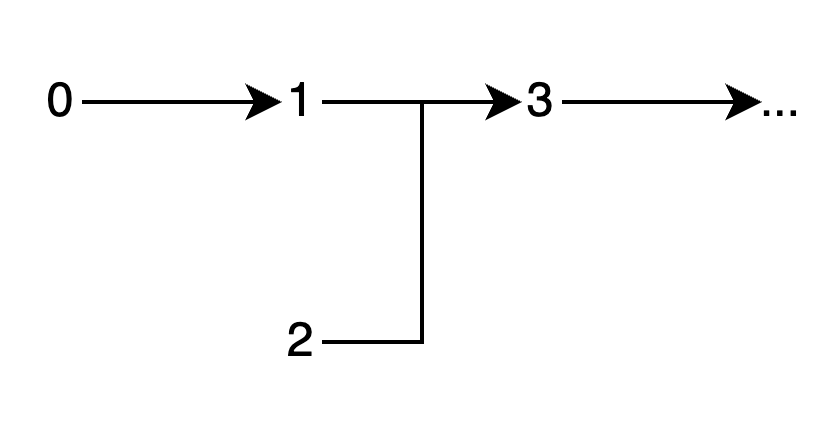
但是,只看公理2的话,自然数增长的”合并“也是可能出现的,如图3所示,1和2的下一个数都是确定的3。所以,公理3就告诉我们,如果1和2的后继数都是3,那么1和2其实是相等的,但很明显$1≠2$,所以这种”合并“的增长也不会出现了。
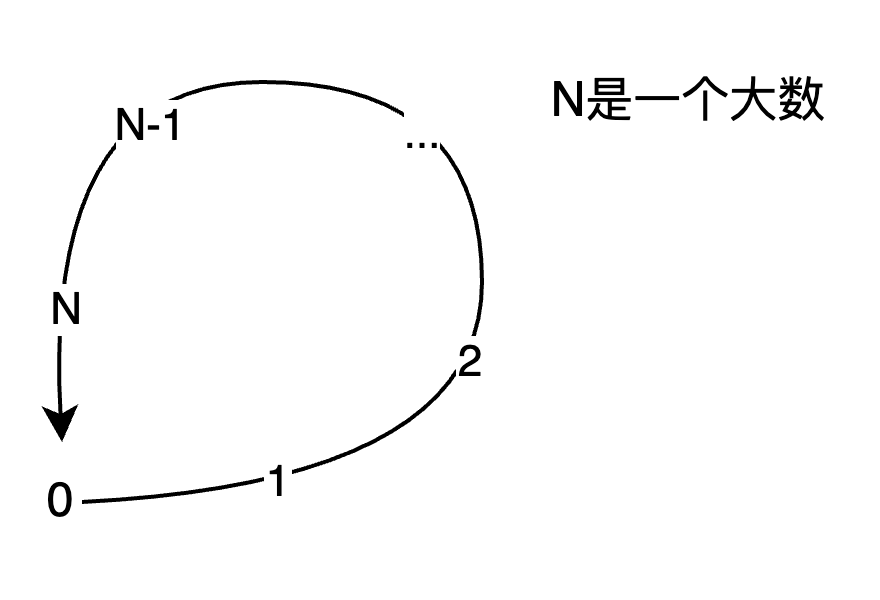
那么,环形的增长呢?如图4所示,某个大数$N$的后继数是0时,公理2和3也是满足的。所以在公理4中,我们严格规定了0不能是任何自然数的后继数,因此,自然数的增长也不能是“环状”的了。
最后,为了限定自然数的外延,防止部分有理数进入自然数的定义(例如0.5等),同时使一些运算在自然数内完备(如加法和乘法,任何两个自然数的加法和乘法操作结果都属于自然数),我们会有公理5。假设没有公理5,那我们可以直接定义$0$和$1$之间有一个“自然数”$0.5$使$S(0)=0.5$,$S(0.5)=1$,然后我们下一步定义加法的时候就会发现,加法对于自然数不完备了($1+0.5=1.5\not\in\mathbb{N}_0$)(当然加法这里我们可以继续定义$1.5,2.5,3.5$等,但如果把加法换成乘法,这里的定义就复杂得多了)这种定义下的自然数便是非标准数学系了
到此为止,自然数被定义,它是一个可数无上界无穷的集合,增长顺序为图1所示。
定义加法
同理,加法也是被定义的:
-
对于任意自然数$m$,$0+m=m$
-
对于任意自然数$m$和$n$,$S(m)+n=S(m+n)$
1+1=2
由加法的第二条定义得知:$1+1=S(0)+1=S(0+1)$
由加法的第一条定义得知:$S(0+1)=S(1)=2$
至此$1+1=2$
更多?
这里再展开一下加法结合律和交换律的证明吧,因为很明显1+1=2的证明并没有用到皮亚诺公理的第五条,这里用结合律和交换律的证明来强化一下第五条的使用
m+0=m
首先证明$m+0=m$,因为在没有交换律的前提下我们并不能得出$0+m=m+0=m$
当$m=0$时,由于加法第一条定义可以得出$0+0=0$,所以成立
假设$m$为$a$时该命题成立,那么我们有$a+0=a$,那么$S(a)+0=S(a+0)=S(a)$,可以证明对于$S(a)$该命题也成立,根据皮亚诺定理,我们可以得知该命题对所有自然数为真
$m+0=m$得证
n+S(m)=S(n+m)
当$n=0$时,$0+S(m)=S(m)=S(0+m)$,成立
假设$n$为$a$时该命题成立,则$a+S(m)=S(a+m)$,那么$S(a)+S(m)=S(a+S(m))=S(S(a+m))=S(S(a)+m)$,可以证明对于$S(a)$该命题也成立,根据皮亚诺定理,我们可以得知该命题对所有自然数为真
结合律
即证明$(a+b)+c=a+(b+c)$
当$c=0$时,$(a+b)+0=a+b=a+(b+0)&,成立
假设$c$为$n$时该命题成立,则$(a+b)+n=a+(b+n)$,那么$(a+b)+S(n)=S((a+b)+n)=S(a+(b+n))=a+S(b+n)=a+(b+S(n))$,可以证明对于$S(n)$也成立,根据皮亚诺定理,我们可以得知该命题对所有自然数为真
交换律
即证明$m+n=n+m$
当$m=0$时,由上面的命题可以得出$0+n=n+0$,所以成立
假设$m$为$a$时该命题成立,那么我们有$a+n=n+a$,那么$S(a)+n=S(a+n)=S(n+a)=n+S(a)$,可以证明对于$S(a)$该命题也成立,根据皮亚诺定理,我们可以得知该命题对所有自然数为真
结语
至此,15年前的我应该也能明白1+1为什么等于2了吧
references
[1] https://www.guokr.com/article/6556/
[2] https://www.zhihu.com/question/23866990/answer/128912950